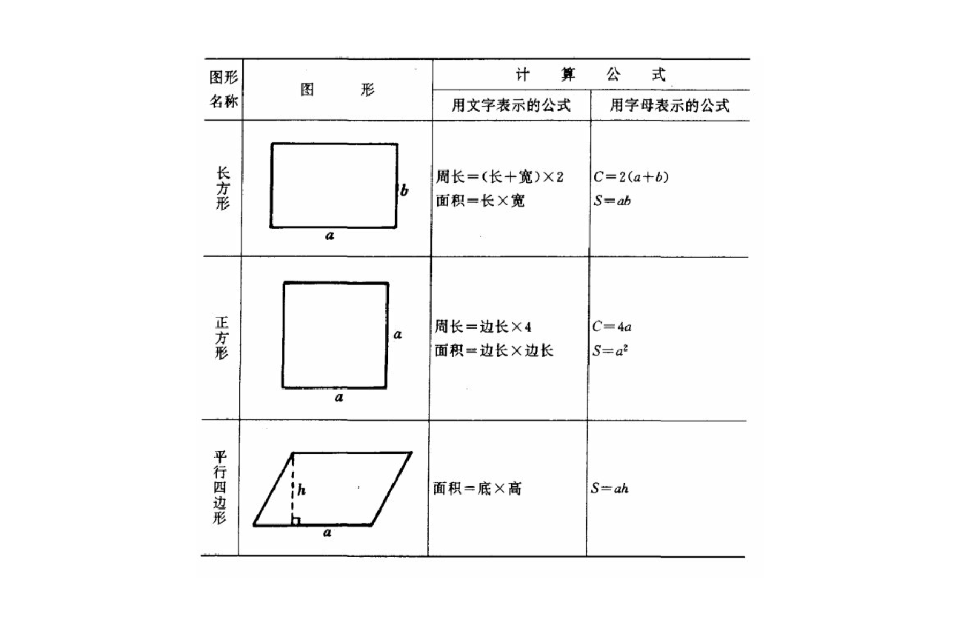
他の面積公式との関係 この面積公式をもとに他の面積公式を導出することができます。 例えば,この公式と正弦定理を用いることで対称な式: S = a b c 4 R S=\dfrac{abc}{4R} S = 4 R ab c を得ることができます( R R R は三角形 A B C ABC A BC の外接円の半径)。 私校資優數學面積題目扇葉形狀 再用方形去減掉兩個角落圓弧形狀,就可以得到第一題的面積。 最後用方形減掉四個刀葉形,就是第二題的面積。 最後,第三題其實就是兩個第二題形狀的面積相加,因為中間重疊,所以再扣掉第三題形狀的面積。 "扇形の弧の長さと面積"の公式とその証明です! 扇形の弧の長さと面積公式扇形の弧の長さと面積半径r、中心角θ、弧の長さl、面積Sとすると \(・l=rθ\) \(・S=\frac{1}{2}r^2θ=\frac{1}{2}lr\)証明
面积公式 搜狗百科
扇 面積 公式
扇 面積 公式-計算結果は問題ないのですが、参考の円弧の長さLの計算式 L=rθですが エクセルで半径×中心角とすると、計算の答えとエクセルの答えが違います。 どちらが正しいかわからないのでググったらL=314×半径×中心角/180という式の答えが 計算結果と同じになりました。 keisanより θの単位はラジアンになります。 単位を度にすると、ご指摘の通り L = 半径×π×中心角 円・扇形の公式まとめ 円周: 2πr 2 π r 円の面積: πr2 π r 2 扇形の弧の長さ: 2πr× a 360 2 π r × a 360 扇形の面積: πr2 × a 360 π r 2 × a 360 扇形の面積(弧の長さ l l からの導出): 1 2lr 1 2 l r ※半径: r r 、円周率: π π 、中心角: a a 、扇形の弧の長さ: l l それぞれについて詳しく見ていきましょう。



1
No003 扇形の面積と円弧の長さ 扇形の面積 A m 2 扇形の角度 θ ° 扇の半径 r m 扇形の面積 A m 2 扇形の角度 θ rad 扇の半径 r m 円弧の長さ l m 扇形の角度 θ ° 扇の半径 r m数学的な記述 中心角 2本の半径がなす角を扇形の中心角という。 中心角が 180° のものは半円であり、円は中心角 360° の扇形と考えることもできる。 円oから、2本の半径oa,obが切り取る扇形を扇形o⌒abと呼ぶ(⌒はabの上にかぶせて書くのが正しい)。 扇 (おうぎ)形の角度を使った面積公式 半 径 半 径 中 心 角 半径 × 半径 × 314 × 中心角 360 ∘
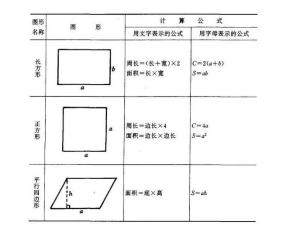
はじめに ここでは、扇の弧の長さとその面積の求め方・公式について説明します。 扇の弧の長さ この図形は、半径が「r」、中心角が「α」、弧の長さが「l」の扇です。このとき扇の弧の長さ「l」は次の公式で求めることができます。 なんで四角形の面積 ・正方形の面積 1辺の長さから正方形の面積を計算します。 ・長方形の面積 縦と横の長さから長方形の面積を計算します。 ・台形の面積 上底と下底、高さから台形の面積を公式を使って計F餘弦定理 1a2=b2c2−2bccosA(已知b,c兩邊長及其夾角∠A,求第三邊長) 2cosA=b 2c2−a2 2bc (已知a,b,c三邊長,求任一內角之餘弦函數值或內角之大小) g三角形的面積公式 ∆ABC之面積=底∗高 2
扇型の面積を求める公式 円の中心角というものを考慮に入れた場合には、扇形の面積は非常に容易に理解することができます。 つまり、扇形の中心角x°を、円の中心角の360°に代入してやれば良いわけです。 扇形の面積=半径×半径×3.14×(x°/360求積公式(平面) a=面積 正方形 長方形 平行四辺形 備考 a寸法はb辺に対し直角に測ったもの 直角三角形 a=面積 鋭角三角形 鈍角三角形 台 形 不平行四辺形 円 a=面積 円分 欠 円 環 形 扇 形円弧面積の計算式 扇形面積=円の面積×( 扇の内角/360°) 三角形の面積=( 半径 2 扇の面積-三角形の面積=円弧の面積 WingneoのIAの計算方法 円弧の始点・終点2点の座標値を丸める。「円弧面積の弦長を求める為の座標丸め」 その2点間距離を求める




初中数学 圆和扇形知识点解读 易考题型归纳



面積公式 常見面積定理 圓公式 扇形公式 圓環面積 三角形公式 海倫公式 坐標公式 中文百科全書
です。 ( π は円周率: π =←無限に長い小数になるからギリシャ文字 π で表すことになっている) 半円の面積は,円の面積の半分だから 3分の1円の面積は,円の面積の3分の1だから 4分の1円の面積は,円の面積の4分の1だから 一般に中心角の扇形の面積は,円の面積のx/360だから 例題1 半径がa (cm2)で中心角が45°の扇形の面積S (cm2)は 例題22つの対角線の長さが $a$、$b$ のひし形の面積 $S$ は、次の公式で求められます。 ひし 形 (がた) の面積 \begin{align*} S = \frac{1}{2} ab \end{align*} 面積 = たての 対角線 (たいかくせん) × 横の対角立体の体積(V),表面積(S)または側面積(F)および重心位置(G) P12 平均自乗誤差 P13 円板の最大応力(σmax)と最大たわみ(ωmax) P96 長柱の座屈 P97 各種断面形の軸のねじり P97 梁の公式 P98 キーの強さ P102 ばねの図表 P111



扇形面积公式推导图 万图壁纸网



扇形面積公式 Geogebra
扇形的弧長與面積 1弧長扇形的弧長我們要怎麼求得呢 2扇形面積 這樣以後題目給我們半徑r,跟角度要我們求扇形的弧長或面積,我們就可以輕鬆的套公式把它算出來了別府扇山ゴルフ倶楽部のホールの特長は、 自然の地形を利用したバラエティに富んだホールです。 適度な難易度に設定されたコースは 初心者から上級者まで、 幅広くお楽しみいただけます。楕円 面積計算 公式 求め方 直径 半径 自動 長軸 短軸



扇形面积怎么求 扇形面积怎么计算 尚书坊



扇形面积计算公式 万图壁纸网
中心角を \(x\) とすると、扇形の面積公式を利用し $$\pi \times 6^2\times \frac{x}{360}=12\pi$$ という方程式を作ることができます。扇(おうぎ)形の面積を求める公式3つと弧の長さの求め方をお伝えします。 面積と弧の長さは比例ですべて解けるのですがこれを苦手にしている中学生はものすごく多いです。 これには当然とも言える理由が3つあります。 ここで図形を認識圓面積公式。 22、求算圓面積。 31、認識扇形及圓心角。 32、能計算簡單的扇形面積。 41、能應用圓面積和圓周長公 式,算出複合圖形的面積的 面積和周長。 1數與量 n312 能對非直線的平面 區域,選定適當的 正方形單位,估計 其概略面積,並檢 驗圓



功課幫



证明扇形面积与弧长公式圆锥的侧面积为什么会等于prl 扇形面积公式推导兀rl 桃丽网
扇形の面積の公式と求め方 扇形の面積の公式は下記です。 S=r 2 θ/2 ※Sは扇形の面積、rは扇形の半径、θは扇形の角度(単位はラジアン) 公式を用いて、例題の扇形の面積を求めましょう。角度60°の扇形があります。半径が6です。面積を求めてください。極方程式の面積 (扇形積分) タイプ: 難関大対策 α α レベル: ★★★★ 極方程式で表される曲線の面積は,通常通り y y を x x で積分するよりもかなり速く求めることができます. 扇形に分割して積分 する方法です.ただし出現頻度はそこまで高くなくおうぎ形の弧の長さ、面積、中心角の求め方と公式 おうぎ形は円を切りとったものです。 半分だけ切りとれば中心角は180°、さらに半分切りとれば中心角は90°になります。 ケーキを半分に切ったり、三分の一にしたりするときを想像するとわかりやすい




扇形面積公式弧長14 Zilhc




扇形面積公式弧長14 Zilhc
扇形のまわりの長さは、 扇形の弧の長さ+半径×2 で求められます。 この扇形の弧の長さ=18×314× 1 ° 360 ° =14(cm) よって、求める扇形のまわりの長さは 14+9×2=3684(cm) 答え 3684㎝ ~平面図形の面積・まわりの長さを求める公式まとめもしくは、単純に、1ラジアンの円弧の長さ(=半径(r))の θ倍であるため ・扇形の面積は (r 2 θ)/2 扇形の面積の公式:円弧×半径/2 に代入 もしくは、円全体の面積 πr 2 に割合 θ/2π を掛ければ 日行一 扇 扇形面積與周長的公式 Youtube 1 3 1 柱体 椎体 台体的表面积1512 1513 1514 图文 百度文库



1
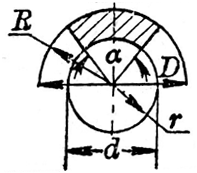



扇环面积计算器 计算专家
扇形面积公式描述了扇形面积和圆心角(顶角)、半径、所对弧长的关系。 数学公式表示为:S扇=(lR)/2 (l为扇形弧长) =(1/2)θR²(θ为以弧度表示的圆心角)。《参考》 1)三角形の面積と重心 2)扇型の面積と重心 3)角錐台の体積と重心 r >孤の長さと面積がわかっていて、半径をxとするとどんな方程式になりますか? 教えてください まずは弧の長さと半径から中心角を計算しよう。 直径x円周率x中心角÷360 = 弧の長さ だね。そのあとに扇型の面積の公式で計算するんだ



细品教材 08年北京奥运会的重要前奏是奥运圣火的传递 圣火由 祥云 火炬承载 传遍五洲四海 宏扬奥林匹克精神 祥云 火炬外型是细长的圆台形式 长72 Cm 重985克 燃料为丙烷 那么在 祥云 的外层着色要覆盖多大的面积 其内部能盛装多少液态的丙烷 本节课



扇形面積 面積公式 另解 公式推導過程 中文百科全書
の2点です。 このポイントは他の問題でも使えるので、ぜひ覚えておきたいですね! すると次のようになるので、 ××314÷4-×÷2=114(cm2) とわかります。 もし、下の図のアとイの面積が等しいことを知っていたら、 イの面積を2倍して 10×10×057 扇形の面積を求める公式は前に述べたとおり以下の公式です。 扇形の面積 = 半径 × 半径 × 円周率 × θ / 360 ・・・ ① 次に弧の長さを求めると以下のようになります。 扇形とは? 面積・中心角・半径・弧の長さの公式と求め方 21年2月19日 この記事では「扇形(おうぎ形)」について、面積の公式や半径・中心角、この長さの求め方をできるだけ簡単に解説していきます。 また、弧度法(ラジアン)で解く計算問題など




面积计算公式 扇形面积计算公式图解正方形面积计算公式好不好 娱乐 略网




扇形の面積の求め方 公式と計算例
V = 体積 (角錐台) S1 = 角錐底面積 S2 = 角錐上面積 球体 V = 体積 A = 球体の表面積 r = 球体半径 楕円体 楕円体の体積 → 楕円体 楕円体の表面積 台形 A = 面積 A = 面積 ヘロンの公式 A = 面積 = bh/2 又は ヘロンの公式 jin 扇の弧の長さと面積の求め方 公式 中学数学 By Okボーイ マナペディア 扇形面積計算公式 扇形面積計算公式 快熱資訊 走進時代 Xbkkvdgkxbkztm



扇形面积公式扇形面积公式是什么 天奇生活




圓的周長與面積 24 如何計算扇形的周長 Youtube




弧長公式三角函數三角函數 Thomblake



Q Tbn And9gctoaftep Cp0mxb1byahotggx3ub73wafwbkzah7fg7xmsh2anr Usqp Cau




面積公式 面積公式包括扇形面積公式 圓形面積公式 弓形面積公式 菱形面 百科知識中文網




扇形面積公式弧長14 Zilhc



扇形面积计算公式 万图壁纸网



人教版数学九年级上册24 4 弧长和扇形的面积 同步练习 含答案 七七文库www 77wenku Com



求扇形面积 高三网



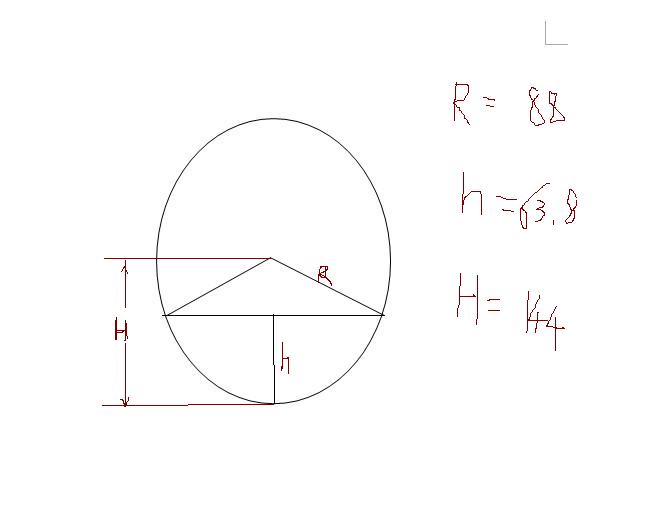
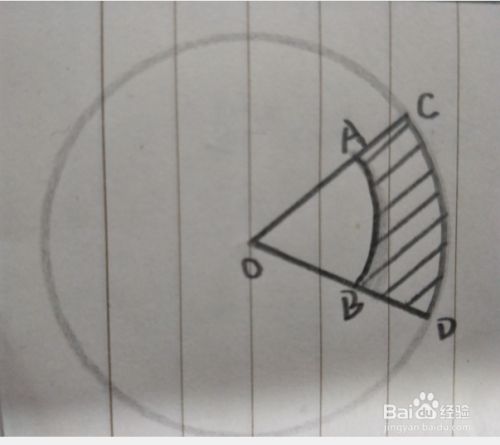
私校資優數學 面積題目 扇葉形狀 Nova的科學反主流學院



计算扇形面积公式有哪些



1 设圆的半径为r圆心角为n度 那么扇形面积s扇形是圆面积s的360分之 扇形的面积公式 1 设圆的半径为r圆心角为n度 那么扇形面积s扇形是圆 面积s的360分之 扇形的面积公式为 S 作业 慧海网



九年级数学上册24 3圆与多边形4弧长扇形面积圆锥表面积计算课件 新人教版 莲山课件




面积公式 搜狗百科



面积公式大全笔记 西瓜视频搜索




扇形面積計算公式第二章三角函數 rbmi



1



梯形的面积推导过程图 信息评鉴中心 酷米资讯 Kumizx Com



数学 扇形面积怎么推导来的 定积分求双纽线面积要用到 扇形面积角度积分公式 德涵网



面积公式 搜狗百科



扇环 快懂百科




面积公式 搜狗百科




扇形面积的计算公式 扇形的面积计算公式




扇形面积怎么算怎样求扇形的面积




扇形面积的计算公式 扇形的面积计算公式



扇环面积公式推导图解 表情大全



圆的面积公式推导 万图壁纸网



扇环面积公式怎么推出的 百度经验



扇形面积公式讲解 北京爱智康




扇形面積為何如此計算呢 Isdp08am 隨意窩xuite日誌




面積公式 面積公式包括扇形面積共式 圓形面積公式 弓形面積公式 菱形面積公 華人百科




扇形の面積公式が一目でわかる 丁寧な証明付き 高校生向け受験応援メディア 受験のミカタ



数学中扇形的面积公式是什么 初三网



扇形的面积公式扇形的面积公式是什么 天气加



私校資優數學 面積題目 扇葉形狀 Nova的科學反主流學院
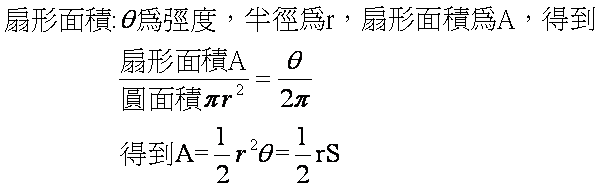



扇形的弧長與面積



Revit教程 如何在revit门明细表中添加面积计算公式 Bim免费教程 腿腿教学网




圓的周長與面積 27 扇形的複合圖行計算2 Youtube



成都初中辅导班扇形面积公式是什么 成都初中辅导班 成都初中补习班 官网
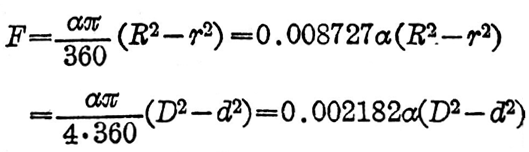



扇环面积计算器 计算专家



扇形面积公式 北大青鸟怎么样 北大青鸟学费多少




扇形面积怎么算怎样求扇形的面积




半圆的面积公式怎么求 半圆的面积怎么求 半圆的面积公式中文




扇形面积的计算公式 扇形的面积计算公式




扇形面積計算計算弧長及扇形的面積 Ttvu




扇形面積公式 公式 推導過程 注意事項 中文百科全書



扇环面积公式推导图解 表情大全




圓面積公式 圓是最重要的曲邊形 古埃及人把它看成是神賜予人的神聖圖形 圓 百科知識中文網




球扇形 球心角体 体积 表面积计算公式与在线计算器 三贝计算网 23bei Com




正三角形高求正三角形的高 Utvos




19 年九年级数学下册3 4 1 弧长和扇形的面积教案二湘教版下载 Word模板 爱问共享资料




Ppt 弧长和扇形面积powerpoint Presentation Free Download Id



扇弧形面积的计算方法 西瓜视频搜索



扇形面积计算公式讲解 北京爱智康



課堂實錄 扇形面積 六上 雪花新闻




例題 扇形的面積計算 數學 均一教育平台



S扇环和s扇的算法 西瓜视频搜索



扇弧形面积的计算方法 西瓜视频搜索



扇形面积扇形面积 面积公式 爱华网



Epqfun8hdfkolm




圆扇形与弓形



弧的周长面积计算公式 学习岛




常用图形面积公式 牛牛文库 海量文档资源分享平台教案课件论文技术总结学习心得doc Ppt Pdf资料



椭圆扇面面积公式本人知道椭圆形面积公式 3 14 A B但不知道椭圆扇面积该如何计算 有那位高手知道椭圆扇形面积公式请指



私校資優數學 面積題目 扇葉形狀 Nova的科學反主流學院




弧長計算公式 弧長公式 N是圓心角度數 R是半徑 L是圓心角弧長 L 華人百科




扇形面积的计算公式 扇形的面积计算公式



课堂实录 扇形面积 六上



Q Tbn And9gcs4mf4ga4ivcw9oaofx1 Zkqgkhy6m1tx85ng7ya0kcksl0rfiq Usqp Cau




扇形面积公式 搜索结果 哔哩哔哩 Bilibili




数学知识 扇形面积公式小学 之间网



扇形的面积公式 图片欣赏中心 急不急图文 Jpjww Com




扇形周長與面積 6年級數學 Grade 6 Math Fan Shaped Area Youtube




扇形面積公式弧長14 Zilhc



扇环面积公式推导图解 表情大全



面積公式 常見面積定理 圓公式 扇形公式 圓環面積 三角形公式 海倫公式 坐標公式 中文百科全書




扇形弧長公式扇形弧長公式1 Qqkaii




高中數學易錯點 重難點系列之 巧記空間幾何體的面積和體積公式 每日頭條




扇形的周长和面积公式是什么




正方形面積對角線2 1 Rimbt




扇の弧の長さと面積の求め方 公式 中学数学 By Okボーイ マナペディア



扇形面积计算公式图解 万图壁纸网




圓錐表面積公式請問圓錐的表面積及體積公式 扇式的面積公式是 Cyujk
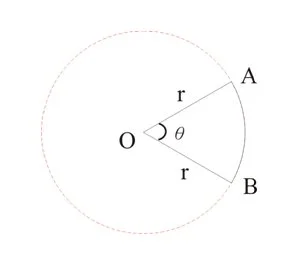



14 平面及立體圖形 扇形的面積及弧長 齊齊溫



计算扇形面积公式有哪些 丑瓜网




Kmb5veidoa4zum



圆锥侧面积公式2 信息评鉴中心 酷米资讯 Kumizx Com



扇形面积计算圆扇形弧形计算公式谁有计算圆弧长扇形面积和圆锥的面积的公式 尚书坊



0 件のコメント:
コメントを投稿