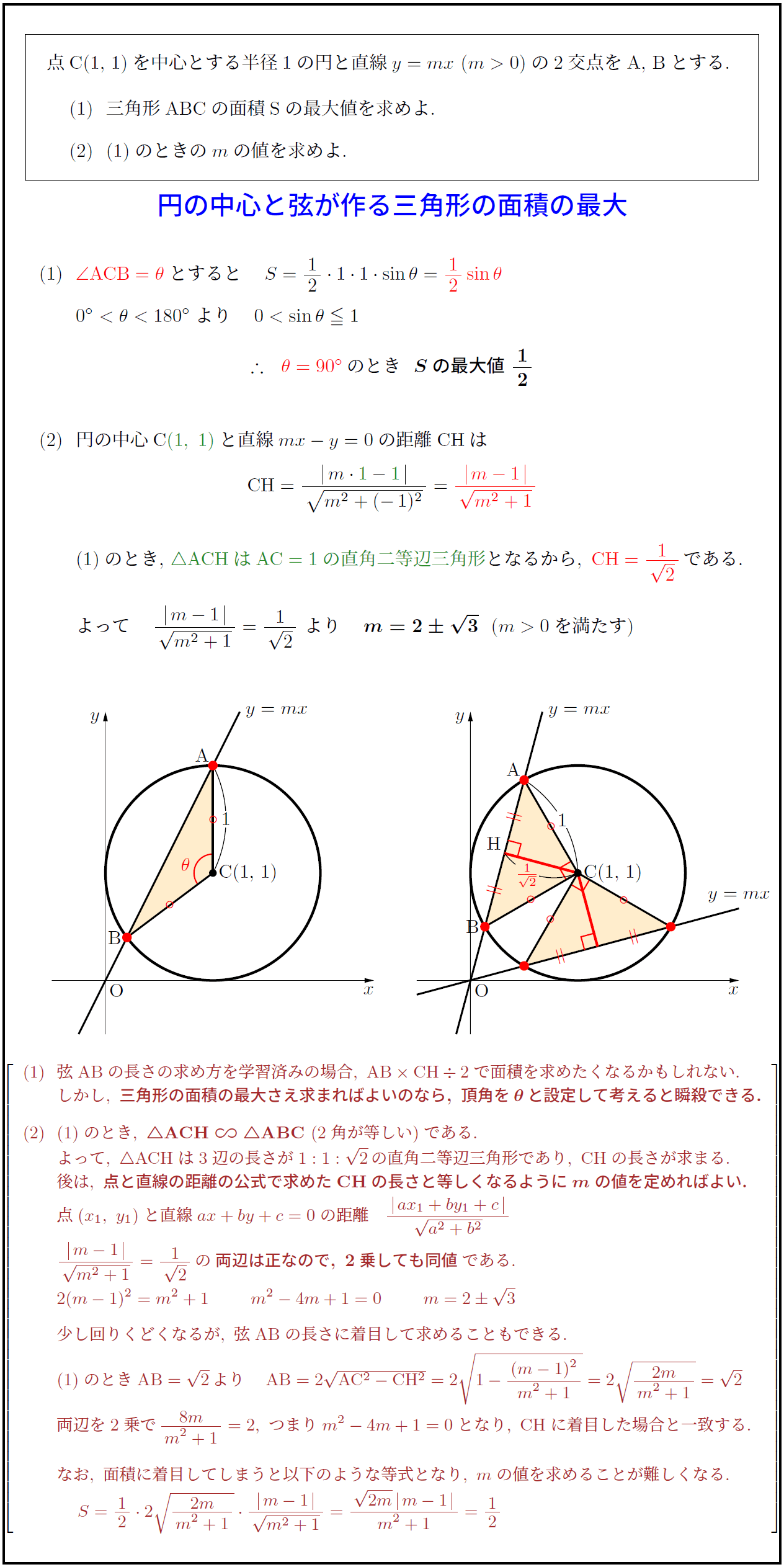
円の方程式の求め方まとめ パターン別に解説するよ 数スタ
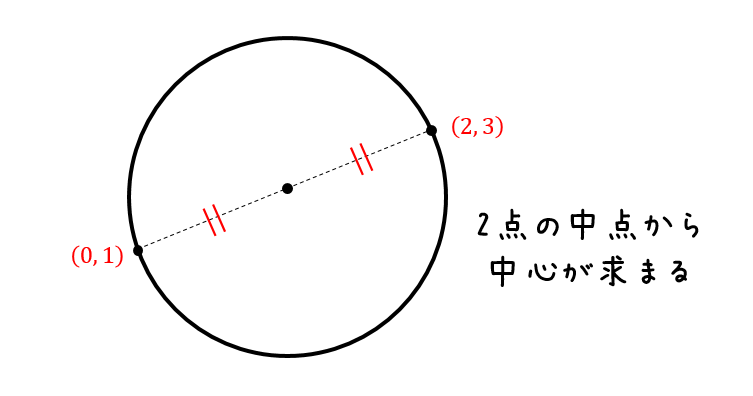
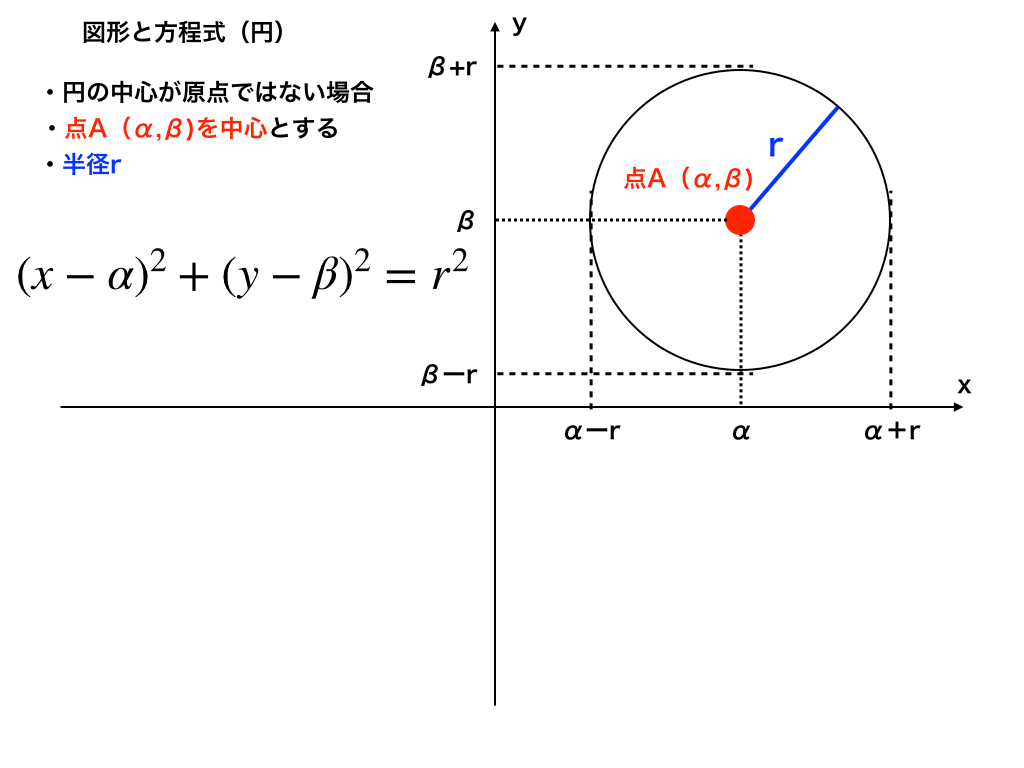
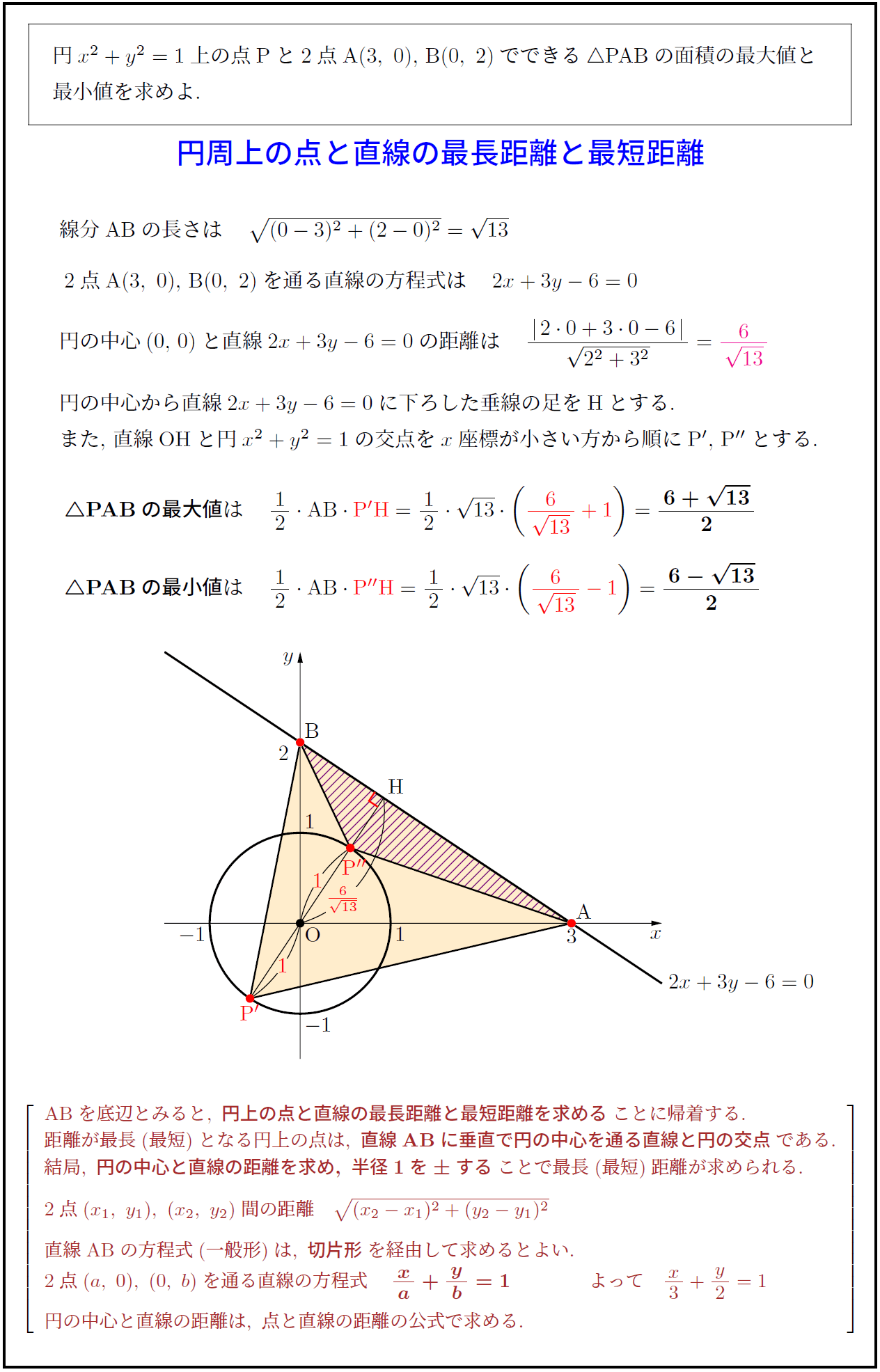
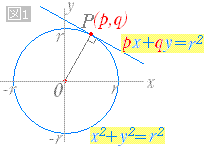
中心が の円の方程式は ① ①が点 を通るので、, を代入して これを①に代入すると、 答え: 例題③「3 点の座標が与えられている」 例題③ 点 、 、 を通る円の方程式を求めなさい。 円が通る 点の座標が与えられている場合は、一般形 を使います。 この式に 点の座標を代入してできた 式を連立して解くと、答えが求められます。 解答 求める円を とおく。 を通るので、 ① を通るので円の方程式の求め方をパターン別に解説 どんな問題であっても、問題文にある条件を公式に代入することで求められます。 では、そのパターンを例題とともに3つ確認してみましょう! まず、確認しておきたいのは円に関する情報の種類についてです
円 中心 求め方 高校
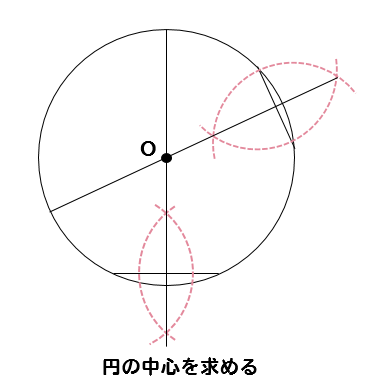
円 中心 求め方 高校-円周上の点はどこでも,円の中心から等距離であるという性質を利用します。 円周上に適当な3つの点を決め,その3点から等距離にある点を作図から求めます。 ここで紹介している内容は17年3月時点の情報です。 ご紹介している内容・名称等は変わる円 円周角の定理の活用 1 次の図の円は、中心がわかっていない。三角定規などの直角を使って、この円の 中心を求めなさい。 367 P o 2 次の図において、点Pを通る円Oの接線を作図しなさい。 ・

中学数学 円の中心の出し方 コンパス編 サクッとわかる なぜか分かる はかせちゃんの怪しい研究室
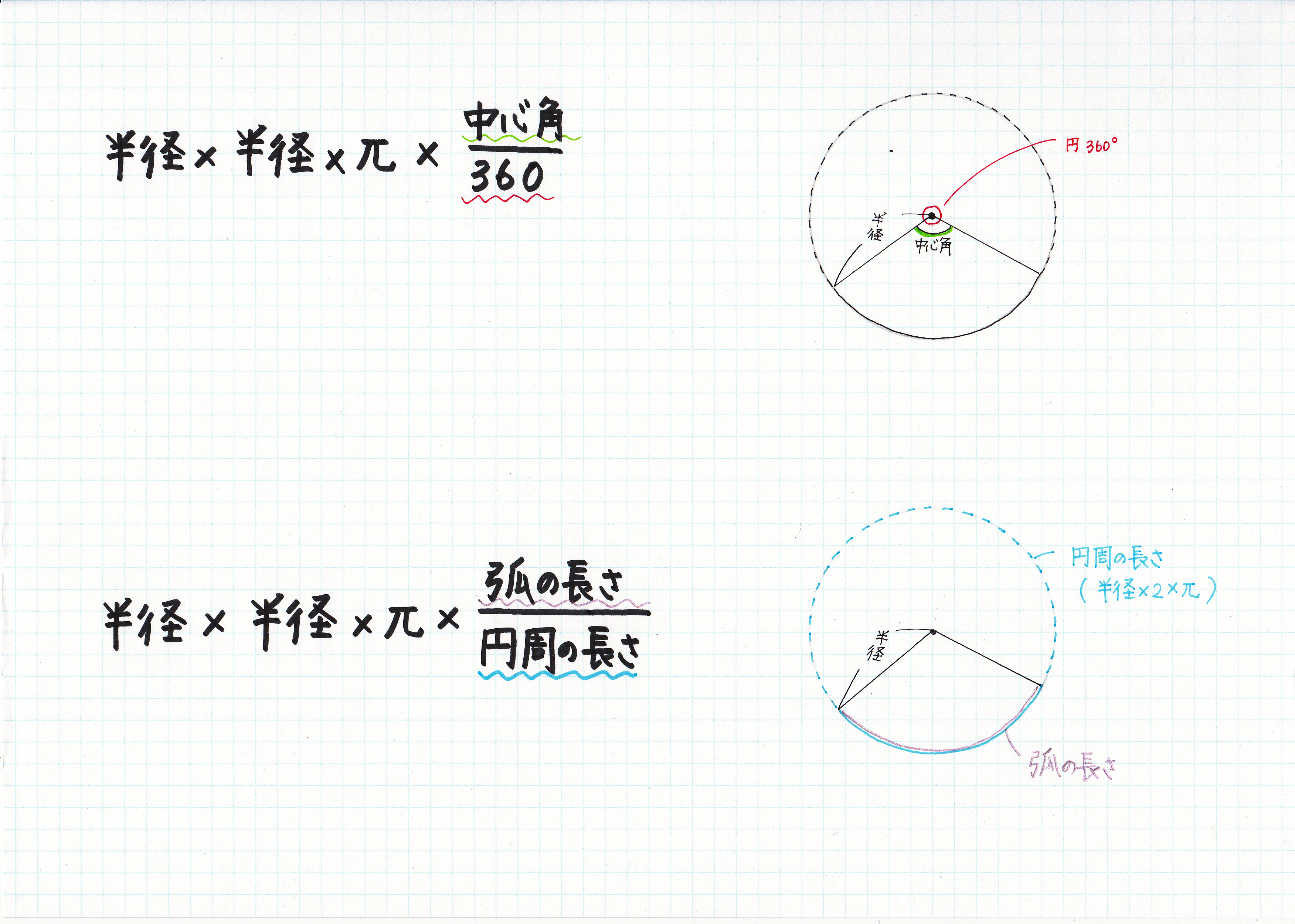
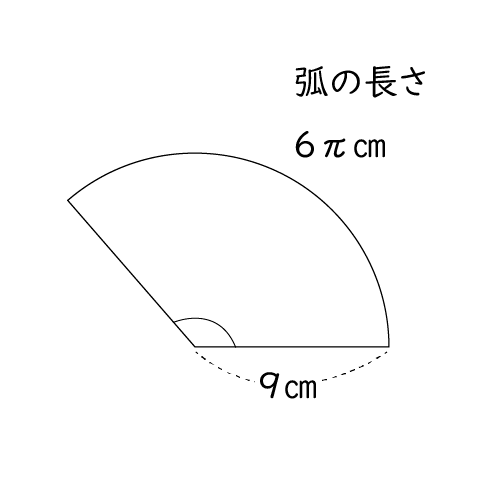
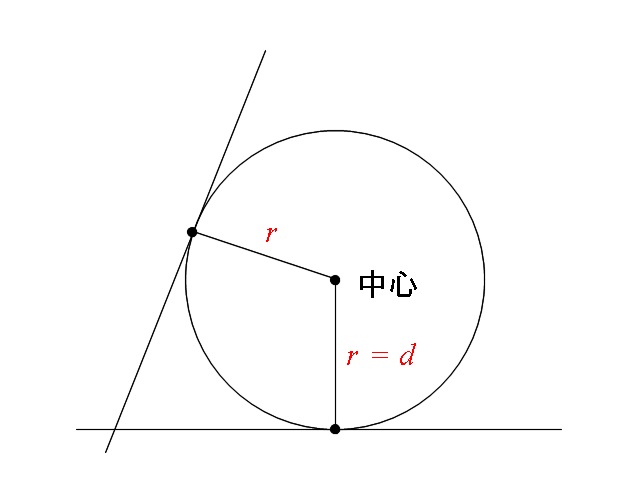
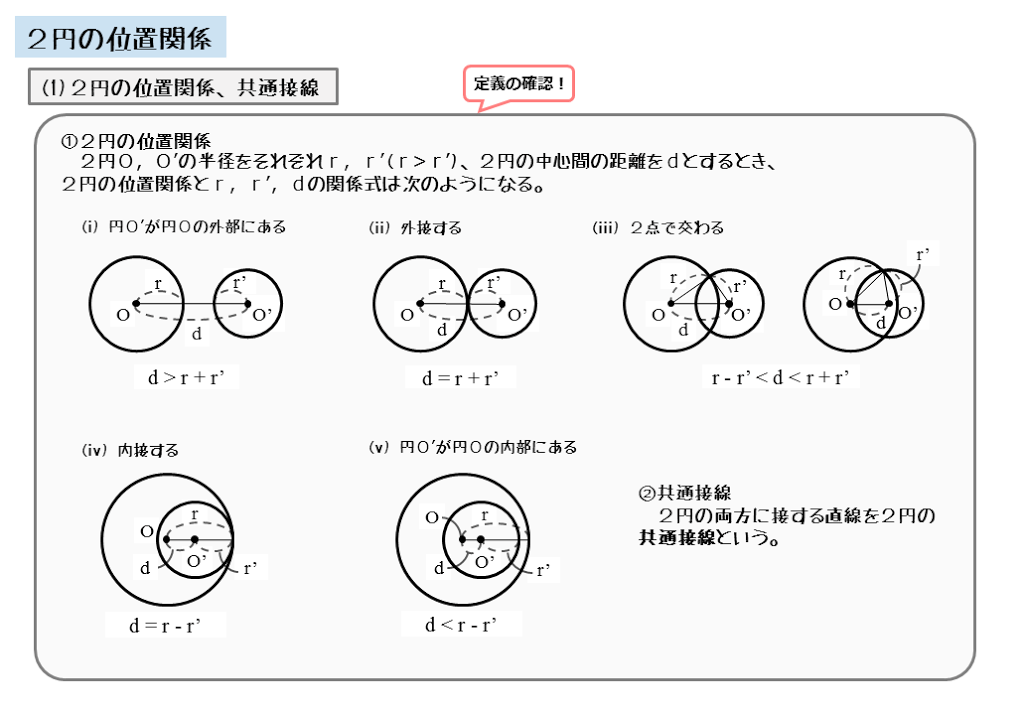
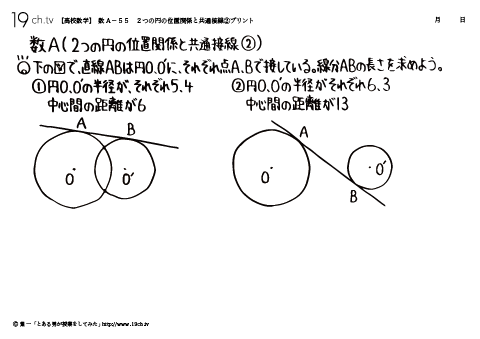
2つの円の位置関係の覚え方 大きさが異なる2つの円の位置関係は5パターンあります。5パターンを丸覚えする必要はありません。 小さい円を真ん中から動かしていけば,5通りが網羅できる と覚えておくとよいです。 5通りの図がスラスラ描けることが重要大きい方の円から小さい方の円の半径を引いても、中心間の距離よりも必ず小さい のです。完全に2つの円の中心が一致している場合を考えるとそれは明らかですね。 中心間の距離は \(0\) ですから、半径同士を引いても \(0\) より小さくはなりませんから。単元:おうぎ型の中心角の解き方 問題 半径9㎝、弧の長さが6n㎝のおうぎ形の中心角を求めなさい。 中学生数学特訓プラン 基礎力養成特訓プラン 推奨学年中学1年~中学3年生内容計算の基礎養成演習時
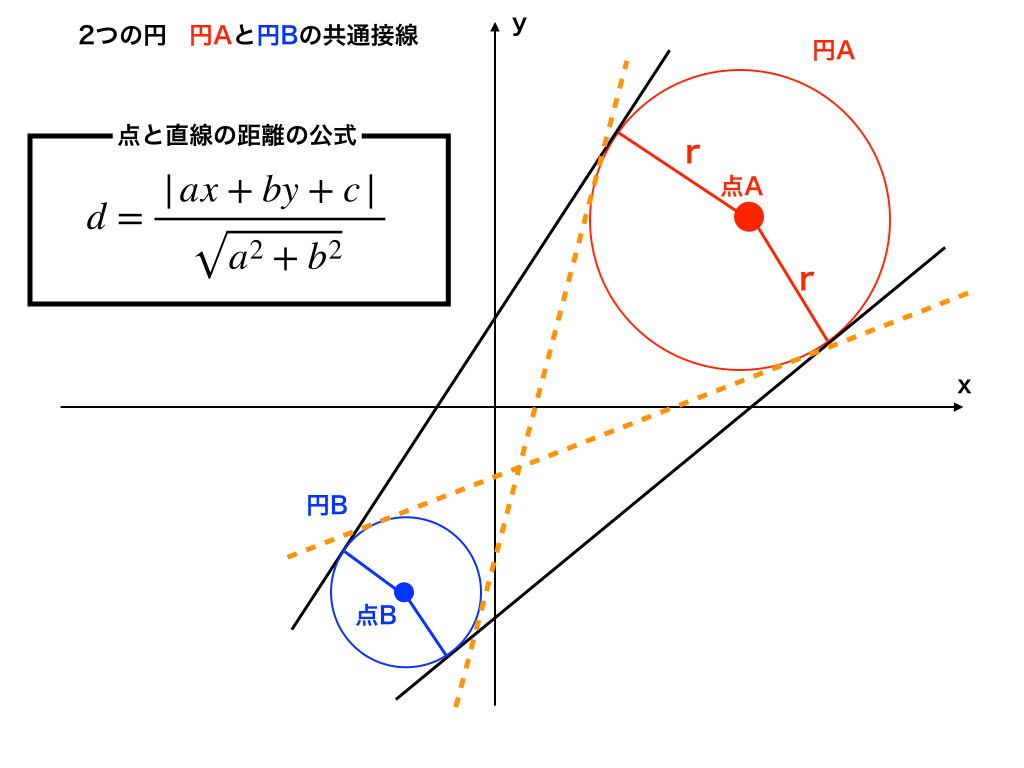
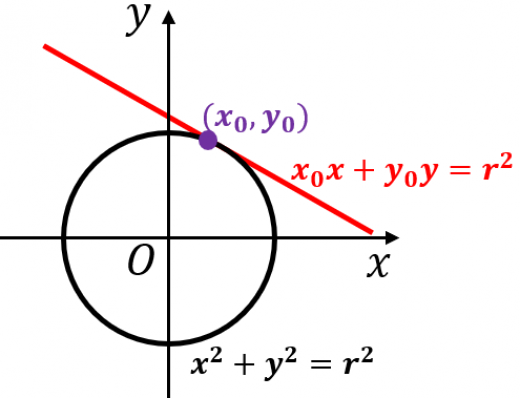
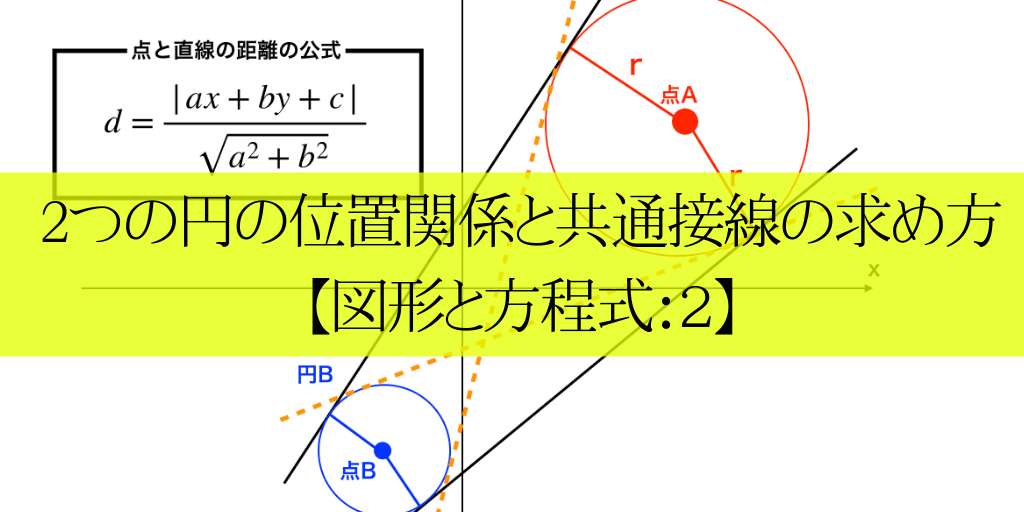
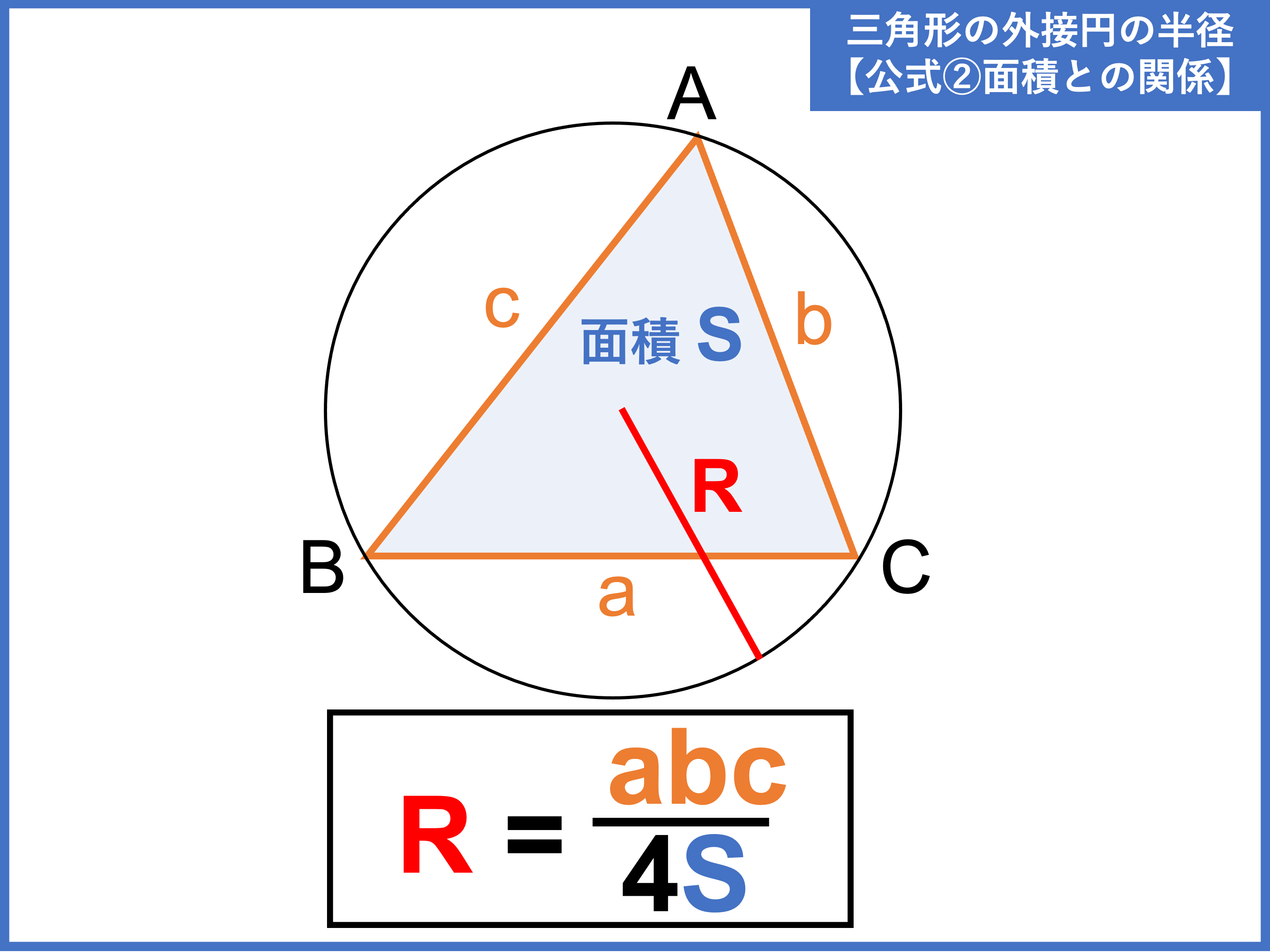
円を選択する 円弧の選択を考える前に、円をマウスで選択することを考えます。 ここでいう選択は、円内部点ではなく、円周上をクリックしたとき「選択された」と考えます。 半径 R、中心点(Cx, Cy)の円を考えます。 これは簡単ですね。外接円の半径・・・ 高校で出し方は習うけど 中学でやったかな・・・ でも高校入試問題で見たことはあるので・・・ (;・∀・) 解き方を説明していきますね では早速問題です ABCの3つの頂点は円Oの周上にあり、AB=√5cm、BC=3cm、CA=2√2cmである3点を通る円POINT 円の通る3点から中心・半径を求める一般式を導出する. 計算フォーム・Excelにコピペして使えるフォーマットもあります. 単純な「連立方程式」の問題ですが,一般解は少し複雑な形になります. 計算フォーム Excel用フォーマット 導出 円の方程式 円の中心 円の
円 中心 求め方 高校のギャラリー
各画像をクリックすると、ダウンロードまたは拡大表示できます
 | ||
 |  |  |
 |  |  |
「円 中心 求め方 高校」の画像ギャラリー、詳細は各画像をクリックしてください。
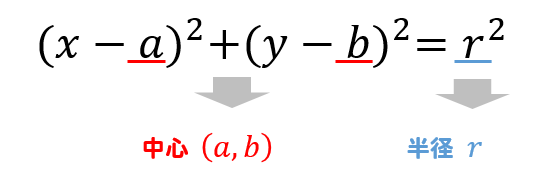 |  |  |
 |  | |
「円 中心 求め方 高校」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  | 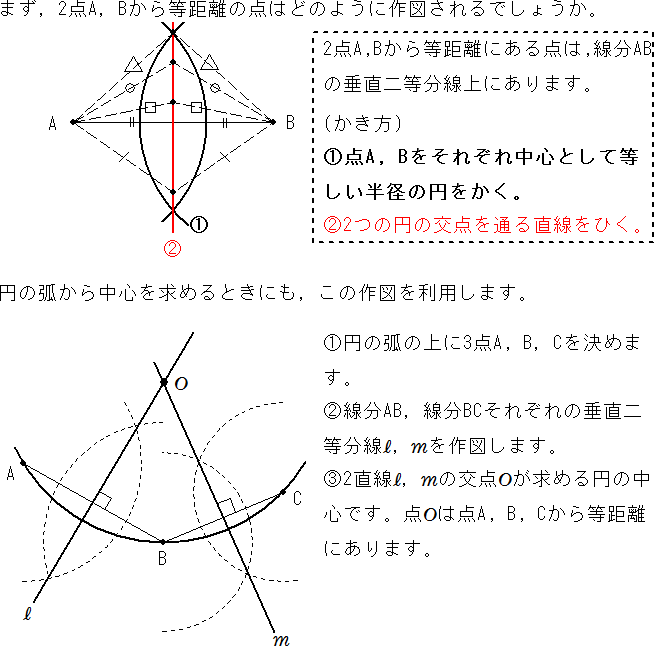 |
 |  |  |
「円 中心 求め方 高校」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  |  |
 |  | |
「円 中心 求め方 高校」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
 |  | |
 |  | |
「円 中心 求め方 高校」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  |  |
 |  |  |
「円 中心 求め方 高校」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  |  |
 |  | |
「円 中心 求め方 高校」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
 |  | |
 |  |  |
「円 中心 求め方 高校」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
 |  |  |
 | ||
「円 中心 求め方 高校」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 | ||
 |  |  |
「円 中心 求め方 高校」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
 |  |  |
 | 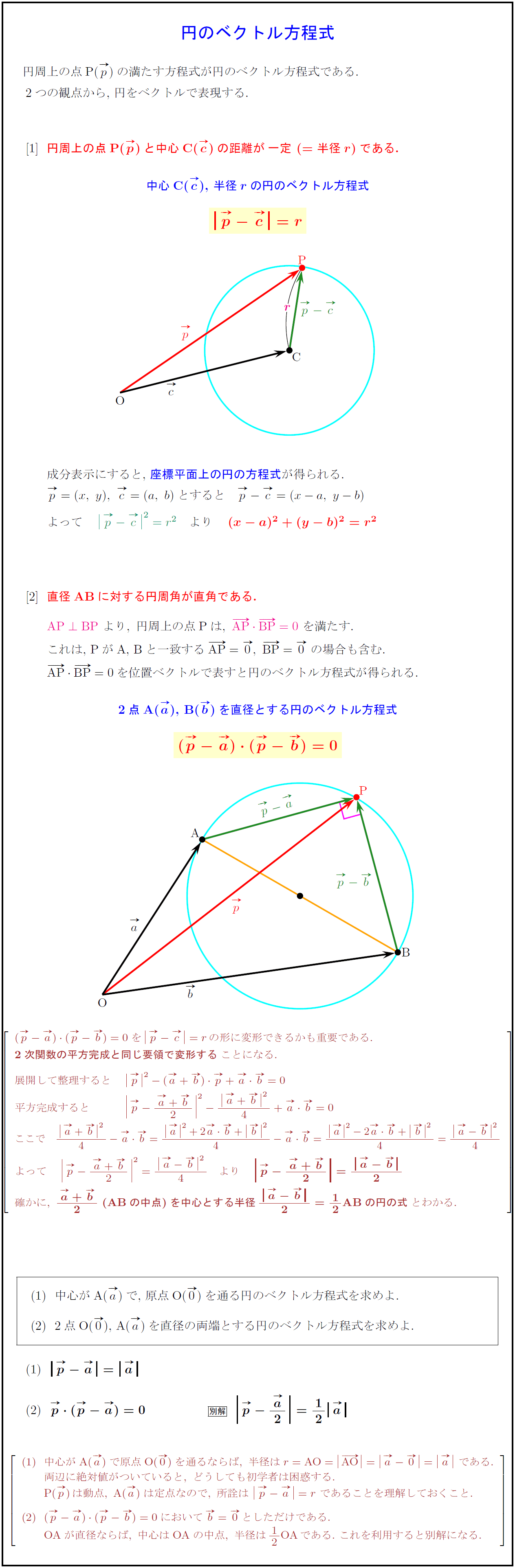 |  |
「円 中心 求め方 高校」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
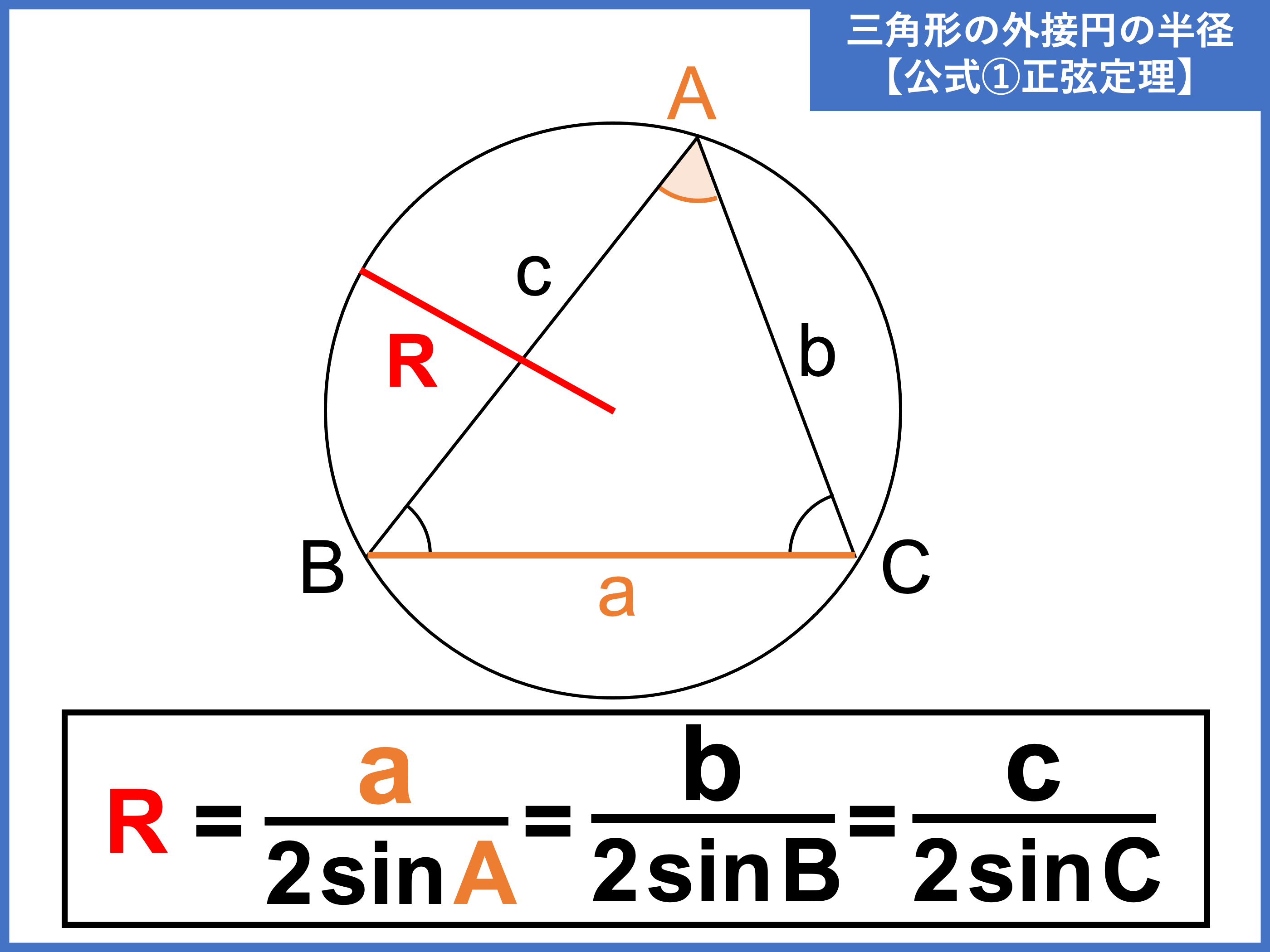 | 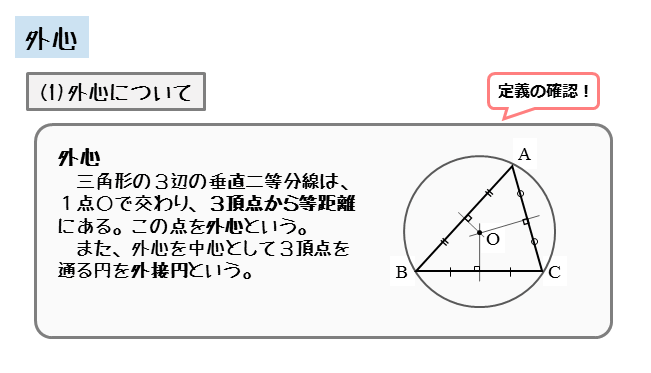 |
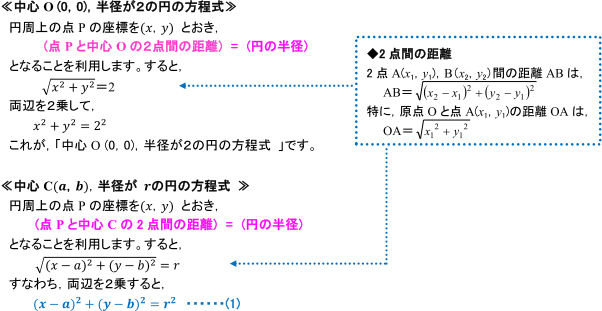
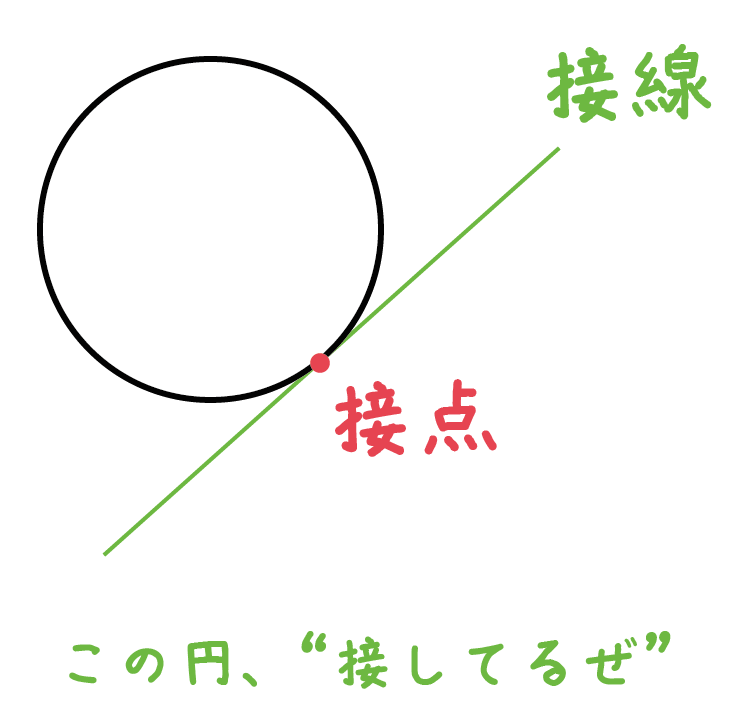
ここで、接点は円上の点なので、 (x - 1)2 (y - 1)2 = 9 に代入しても成り立ちます。 (α- 1)2 (β - 1)2 = 9 ・・・② ①、②式は、α, β の連立方程式と見ることができます。 (なので、連立方程式を解けば、接点 (α, β)が求まります) ①を②に代入して、 (α- 1)2 (\ \frac {173α} {5} \) - 1)2 = 9 これを計算。 整理すると、 17α2 - 61α - 28 = 0 となります。 これは、αの2次方程式で円錐の中心角の求め方概要 扇部分の半径 (母線)・弧の長さを求める (扇の中心角を求める問題になる) 中心角を求める こんな感じだよ 既に知ってる「扇の中心角を求める問題」に変えてしまう っていうのがポイント! 扇の中心角の求め方を知らない人は、 扇形の中心角の求め方3パターン を見てみてね ちなみに、 中心角を求める公式 もあって 中心角 = 360×
Incoming Term: 円 中心 求め方 高校,




0 件のコメント:
コメントを投稿